vtreat cross frames

Example demonstrating “cross validated training frames” (or “cross frames”) in vtreat.

Consider the following data frame. The outcome only depends on the “good” variables, not on the (high degree of freedom) “bad” variables. Modeling such a data set runs a high risk of over-fit.

set.seed(22626)

mkData <- function(n) {
  d <- data.frame(xBad1=sample(paste('level',1:1000,sep=''),n,replace=TRUE),
                  xBad2=sample(paste('level',1:1000,sep=''),n,replace=TRUE),
                  xBad3=sample(paste('level',1:1000,sep=''),n,replace=TRUE),
                  xGood1=rnorm(n),
                  xGood2=rnorm(n))
  
  # outcome only depends on "good" variables
  d$y <- rnorm(nrow(d))+0.2*d$xGood1 + 0.3*d$xGood2>0.5
  # the random group used for splitting the data set, not a variable.
  d$rgroup <- sample(c("cal","train","test"),nrow(d),replace=TRUE)  
  d
}

d <- mkData(2000)

# devtools::install_github("WinVector/WVPlots")
# library('WVPlots')
plotRes <- function(d,predName,yName,title) {
  print(title)
  tab <- table(truth=d[[yName]],pred=d[[predName]]>0.5)
  print(tab)
  diag <- sum(vapply(seq_len(min(dim(tab))),
                     function(i) tab[i,i],numeric(1)))
  acc <- diag/sum(tab)
#  if(requireNamespace("WVPlots",quietly=TRUE)) {
#     print(WVPlots::ROCPlot(d,predName,yName,title))
#  }
  print(paste('accuracy',acc))
}

The Wrong Way

Bad practice: use the same set of data to prepare variable encoding and train a model.

dTrain <- d[d$rgroup!='test',,drop=FALSE]
dTest <- d[d$rgroup=='test',,drop=FALSE]
treatments <- vtreat::designTreatmentsC(dTrain,c('xBad1','xBad2','xBad3','xGood1','xGood2'),
                                        'y',TRUE,
  rareCount=0 # Note: usually want rareCount>0, setting to zero to illustrate problem
)

## [1] "vtreat 1.6.3 inspecting inputs Fri Jun 11 07:01:37 2021"
## [1] "designing treatments Fri Jun 11 07:01:37 2021"
## [1] " have initial level statistics Fri Jun 11 07:01:37 2021"
## [1] " scoring treatments Fri Jun 11 07:01:37 2021"
## [1] "have treatment plan Fri Jun 11 07:01:37 2021"
## [1] "rescoring complex variables Fri Jun 11 07:01:37 2021"
## [1] "done rescoring complex variables Fri Jun 11 07:01:38 2021"

dTrainTreated <- vtreat::prepare(treatments,dTrain,
  pruneSig=c() # Note: usually want pruneSig to be a small fraction, setting to null to illustrate problems
)

## Warning in prepare.treatmentplan(treatments, dTrain, pruneSig = c()):
## possibly called prepare() on same data frame as designTreatments*()/
## mkCrossFrame*Experiment(), this can lead to over-fit. To avoid this, please use
## mkCrossFrame*Experiment$crossFrame.

f <- wrapr::mk_formula("y", treatments$scoreFrame$varName)
print(f)

## y ~ xBad1_catP + xBad1_catB + xBad2_catP + xBad2_catB + xBad3_catP + 
##     xBad3_catB + xGood1 + xGood2
## <environment: base>

m1 <- glm(f,
          data=dTrainTreated,family=binomial(link='logit'))

## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred

print(summary(m1))  # notice low residual deviance

## 
## Call:
## glm(formula = f, family = binomial(link = "logit"), data = dTrainTreated)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -2.258   0.000   0.000   0.000   1.970  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)   -6.5366     2.4568  -2.661 0.007801 ** 
## xBad1_catP  1168.1918   645.3595   1.810 0.070274 .  
## xBad1_catB     1.8573     0.7867   2.361 0.018228 *  
## xBad2_catP   167.4370   389.0529   0.430 0.666926    
## xBad2_catB     1.4484     0.5456   2.655 0.007936 ** 
## xBad3_catP   545.7586   453.9221   1.202 0.229240    
## xBad3_catB     2.5985     0.6799   3.822 0.000133 ***
## xGood1         0.7846     0.3519   2.229 0.025792 *  
## xGood2         0.2889     0.3102   0.931 0.351838    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1662.745  on 1332  degrees of freedom
## Residual deviance:   86.371  on 1324  degrees of freedom
## AIC: 104.37
## 
## Number of Fisher Scoring iterations: 13

dTrain$predM1 <- predict(m1,newdata=dTrainTreated,type='response')
plotRes(dTrain,'predM1','y','model1 on train')

## [1] "model1 on train"
##        pred
## truth   FALSE TRUE
##   FALSE   898   14
##   TRUE      6  415
## [1] "accuracy 0.984996249062266"

dTestTreated <- vtreat::prepare(treatments,dTest,pruneSig=c())
dTest$predM1 <- predict(m1,newdata=dTestTreated,type='response')
plotRes(dTest,'predM1','y','model1 on test')

## [1] "model1 on test"
##        pred
## truth   FALSE TRUE
##   FALSE   356  119
##   TRUE    147   45
## [1] "accuracy 0.60119940029985"

Notice above that we see a training accuracy of 98% and a test accuracy of 60%. Also notice the downstream model (the glm) erroneously thinks the xBad?_cat variables are significant (due to the large number of degrees of freedom hidden from the downstream model by the impact/effect coding).

The Right Way: A Calibration Set

Now try a proper calibration/train/test split:

dCal <- d[d$rgroup=='cal',,drop=FALSE]
dTrain <- d[d$rgroup=='train',,drop=FALSE]
dTest <- d[d$rgroup=='test',,drop=FALSE]

# a nice heuristic, 
# expect only a constant number of noise variables to sneak past
pruneSig <- 1/ncol(dTrain) 
treatments <- vtreat::designTreatmentsC(dCal,
                                        c('xBad1','xBad2','xBad3','xGood1','xGood2'),
                                        'y',TRUE,
  rareCount=0 # Note: usually want rareCount>0, setting to zero to illustrate problem
)

## [1] "vtreat 1.6.3 inspecting inputs Fri Jun 11 07:01:38 2021"
## [1] "designing treatments Fri Jun 11 07:01:38 2021"
## [1] " have initial level statistics Fri Jun 11 07:01:38 2021"
## [1] " scoring treatments Fri Jun 11 07:01:38 2021"
## [1] "have treatment plan Fri Jun 11 07:01:38 2021"
## [1] "rescoring complex variables Fri Jun 11 07:01:38 2021"
## [1] "done rescoring complex variables Fri Jun 11 07:01:38 2021"

dTrainTreated <- vtreat::prepare(treatments,dTrain,
  pruneSig=pruneSig)
newvars <- setdiff(colnames(dTrainTreated),'y')
m1 <- glm(paste('y',paste(newvars,collapse=' + '),sep=' ~ '),
          data=dTrainTreated,family=binomial(link='logit'))
print(summary(m1))

## 
## Call:
## glm(formula = paste("y", paste(newvars, collapse = " + "), sep = " ~ "), 
##     family = binomial(link = "logit"), data = dTrainTreated)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -1.856  -0.899  -0.686   1.195   2.218  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  -0.77344    0.16769  -4.612 3.98e-06 ***
## xBad1_catP  -21.99731  108.37126  -0.203    0.839    
## xBad2_catB    0.00254    0.01552   0.164    0.870    
## xGood1        0.45161    0.08974   5.032 4.84e-07 ***
## xGood2        0.54021    0.09028   5.984 2.18e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 860.31  on 677  degrees of freedom
## Residual deviance: 798.35  on 673  degrees of freedom
## AIC: 808.35
## 
## Number of Fisher Scoring iterations: 4

dTrain$predM1 <- predict(m1,newdata=dTrainTreated,type='response')
plotRes(dTrain,'predM1','y','model1 on train')

## [1] "model1 on train"
##        pred
## truth   FALSE TRUE
##   FALSE   424   30
##   TRUE    172   52
## [1] "accuracy 0.702064896755162"

dTestTreated <- vtreat::prepare(treatments,dTest,
                                pruneSig=pruneSig)
dTest$predM1 <- predict(m1,newdata=dTestTreated,type='response')
plotRes(dTest,'predM1','y','model1 on test')

## [1] "model1 on test"
##        pred
## truth   FALSE TRUE
##   FALSE   436   39
##   TRUE    154   38
## [1] "accuracy 0.710644677661169"

Notice above that we now see training and test accuracies of 70%. We have defeated over-fit in two ways: training performance is closer to test performance, and test performance is better. Also we see that the model now properly considers the “bad” variables to be insignificant.

Another Right Way: Cross-Validation

Below is a more statistically efficient practice: building a cross training frame.

The intuition

Consider any trained statistical model (in this case our treatment plan and variable selection plan) as a two-argument function f(A,B). The first argument is the training data and the second argument is the application data. In our case f(A,B) is: designTreatmentsC(A) %>% prepare(B), and it produces a treated data frame.

When we use the same data in both places to build our training frame, as in

TrainTreated = f(TrainData,TrainData),

we are not doing a good job simulating the future application of f(,), which will be f(TrainData,FutureData).

To improve the quality of our simulation we can call

TrainTreated = f(CalibrationData,TrainData)

where CalibrationData and TrainData are disjoint datasets (as we did in the earlier example) and expect this to be a good imitation of future f(CalibrationData,FutureData).

Cross-Validation and vtreat: The cross-frame.

Another approach is to build a “cross validated” version of f. We split TrainData into a list of 3 disjoint row intervals: Train1,Train2,Train3. Instead of computing f(TrainData,TrainData) compute:

TrainTreated = f(Train2+Train3,Train1) + f(Train1+Train3,Train2) + f(Train1+Train2,Train3)

(where + denotes rbind()).

The idea is this looks a lot like f(TrainData,TrainData) except it has the important property that no row in the right-hand side is ever worked on by a model built using that row (a key characteristic that future data will have) so we have a good imitation of f(TrainData,FutureData).

In other words: we use cross validation to simulate future data. The main thing we are doing differently is remembering that we can apply cross validation to any two argument function f(A,B) and not only to functions of the form f(A,B) = buildModel(A) %>% scoreData(B). We can use this formulation in stacking or super-learning with f(A,B) of the form buildSubModels(A) %>% combineModels(B) (to produce a stacked or ensemble model); the idea applies to improving ensemble methods in general.

See:

“General oracle inequalities for model selection” Charles Mitchell and Sara van de Geer
“On Cross-Validation and Stacking: Building seemingly predictive models on random data” Claudia Perlich and Grzegorz Swirszcz
“Super Learner” Mark J. van der Laan, Eric C. Polley, and Alan E. Hubbard

In fact you can think of vtreat as a super-learner.

In super learning cross validation techniques are used to simulate having built sub-model predictions on novel data. The simulated out of sample-applications of these sub models (and not the sub models themselves) are then used as input data for the next stage learner. In future application the actual sub-models are applied and their immediate outputs is used by the super model.

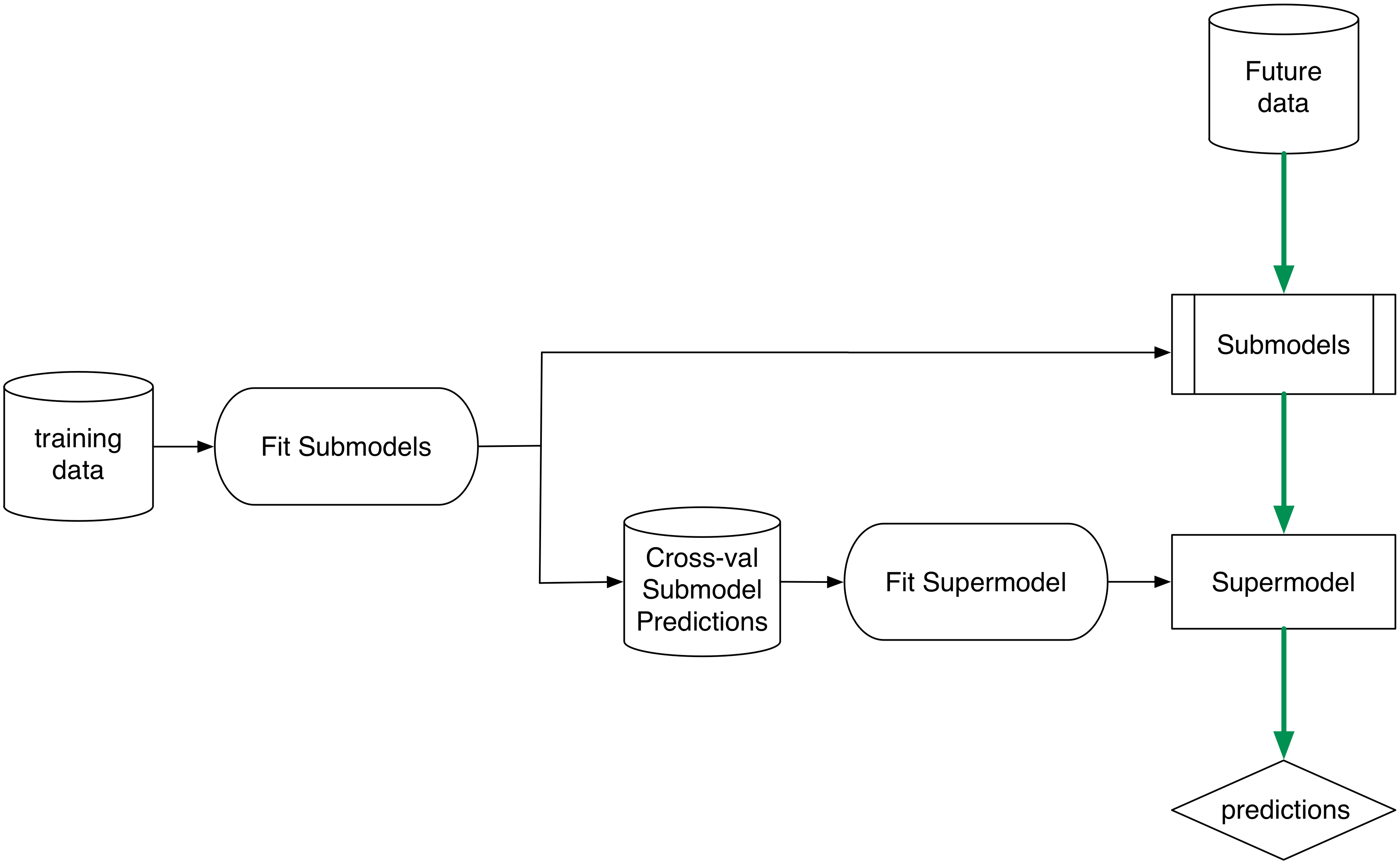
In vtreat the sub-models are single variable treatments and the outer model construction is left to the practitioner (using the cross-frames for simulation and not the treatmentplan). In application the treatment plan is used.

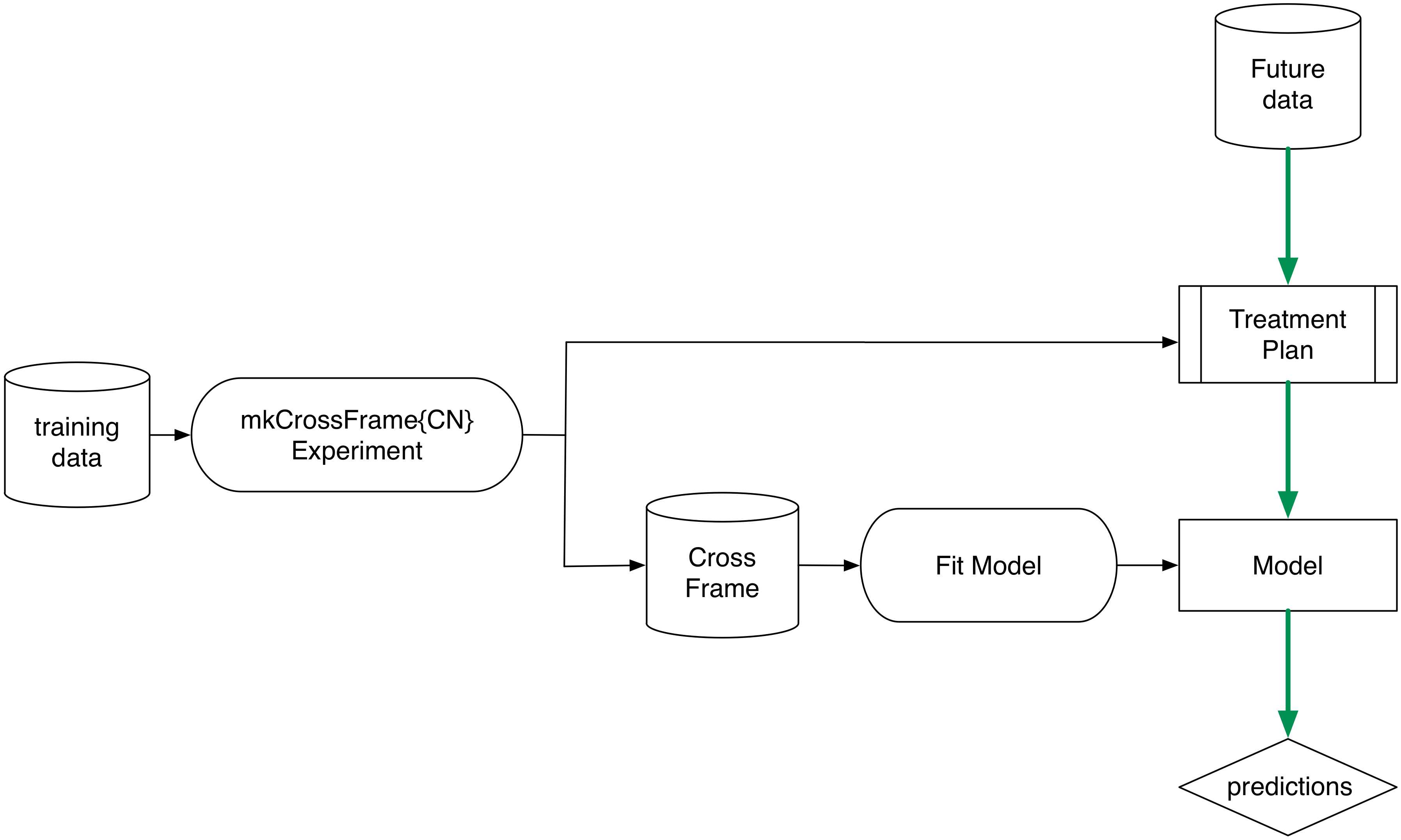
Example

Below is the example cross-run. The function mkCrossFrameCExperiment returns a treatment plan for use in preparing future data, and a cross-frame for use in fitting a model.

dTrain <- d[d$rgroup!='test',,drop=FALSE]
dTest <- d[d$rgroup=='test',,drop=FALSE]
prep <- vtreat::mkCrossFrameCExperiment(dTrain,
           c('xBad1','xBad2','xBad3','xGood1','xGood2'),
           'y',TRUE,
           rareCount=0 # Note: usually want rareCount>0, setting to zero to illustrate problems
)

## [1] "vtreat 1.6.3 start initial treatment design Fri Jun 11 07:01:38 2021"
## [1] " start cross frame work Fri Jun 11 07:01:38 2021"
## [1] " vtreat::mkCrossFrameCExperiment done Fri Jun 11 07:01:39 2021"

treatments <- prep$treatments

knitr::kable(treatments$scoreFrame[,c('varName','sig')])

varName	sig
xBad1_catP	0.8486902
xBad1_catB	0.1386407
xBad2_catP	0.9320211
xBad2_catB	0.7982378
xBad3_catP	0.8604189
xBad3_catB	0.1007443
xGood1	0.0000000
xGood2	0.0000000

colnames(prep$crossFrame)

## [1] "xBad1_catP" "xBad1_catB" "xBad2_catP" "xBad2_catB" "xBad3_catP"
## [6] "xBad3_catB" "xGood1"     "xGood2"     "y"

# vtreat::mkCrossFrameCExperiment doesn't take a pruneSig argument, but we can
# prune on our own.
print(pruneSig)

## [1] 0.1428571

newvars <- treatments$scoreFrame$varName[treatments$scoreFrame$sig<=pruneSig]
# force in bad variables, to show we "belt and suspenders" deal with them
# in that things go well in the cross-frame even if they sneak past pruning
newvars <- sort(union(newvars,c("xBad1_catB","xBad2_catB","xBad3_catB")))
print(newvars)

## [1] "xBad1_catB" "xBad2_catB" "xBad3_catB" "xGood1"     "xGood2"

dTrainTreated <- prep$crossFrame

We ensured the undesirable xBad*_catB variables back in to demonstrate that even if they sneak past a lose pruneSig, the crossframe lets the downstream model deal with them correctly. To ensure more consistent filtering of the complicated variables one can increase the ncross argument in vtreat::mkCrossFrameCExperiment/vtreat::mkCrossFrameNExperiment.

Now we fit the model to the cross-frame rather than to prepare(treatments, dTrain) (the treated training data).

m1 <- glm(paste('y',paste(newvars,collapse=' + '),sep=' ~ '),
          data=dTrainTreated,family=binomial(link='logit'))
print(summary(m1))

## 
## Call:
## glm(formula = paste("y", paste(newvars, collapse = " + "), sep = " ~ "), 
##     family = binomial(link = "logit"), data = dTrainTreated)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.6349  -0.8718  -0.6592   1.1632   2.2616  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.823469   0.069357 -11.873  < 2e-16 ***
## xBad1_catB  -0.027023   0.010167  -2.658  0.00786 ** 
## xBad2_catB   0.007309   0.009871   0.740  0.45907    
## xBad3_catB   0.031346   0.010194   3.075  0.00211 ** 
## xGood1       0.390686   0.063926   6.111 9.87e-10 ***
## xGood2       0.514013   0.064541   7.964 1.66e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1662.7  on 1332  degrees of freedom
## Residual deviance: 1535.9  on 1327  degrees of freedom
## AIC: 1547.9
## 
## Number of Fisher Scoring iterations: 3

dTrain$predM1 <- predict(m1,newdata=dTrainTreated,type='response')
plotRes(dTrain,'predM1','y','model1 on train')

## [1] "model1 on train"
##        pred
## truth   FALSE TRUE
##   FALSE   858   54
##   TRUE    325   96
## [1] "accuracy 0.715678919729932"

dTestTreated <- vtreat::prepare(treatments,dTest,
                                pruneSig=c(),varRestriction=newvars)
knitr::kable(head(dTestTreated))

xBad1_catB	xBad2_catB	xBad3_catB	xGood1	xGood2	y
0.773007	-0.3255386	0.0000000	-1.5105399	-0.6111387	FALSE
0.000000	-8.4374333	-9.1305305	-1.2629291	2.0045631	TRUE
9.983447	0.7730070	0.0000000	0.1323056	-0.1780657	FALSE
0.773007	0.0000000	10.6765446	-1.8673372	1.3348230	FALSE
-8.437433	0.0000000	-9.1305305	0.2635566	0.4006814	FALSE
-9.535979	0.7730070	0.0799098	0.3260325	1.4338856	FALSE

dTest$predM1 <- predict(m1,newdata=dTestTreated,type='response')
plotRes(dTest,'predM1','y','model1 on test')

## [1] "model1 on test"
##        pred
## truth   FALSE TRUE
##   FALSE   438   37
##   TRUE    163   29
## [1] "accuracy 0.700149925037481"

We again get the better 70% test accuracy. And this is a more statistically efficient technique as we didn’t have to restrict some data to calibration.

The model fit to the cross-frame behaves similarly to the model produced via the process f(CalibrationData, TrainData). Notice that the xBad*_catB variables fail to achieve significance in the downstream glm model, allowing that model to give them small coefficients and even (if need be) prune them out. This is the point of using a cross frame as we see in the first example the xBad*_catB are hard to remove if they make it to standard (non-cross) frames as they are hiding a lot of degrees of freedom from downstream modeling procedures.