Plot the cumulative gain curve of a sort-order.

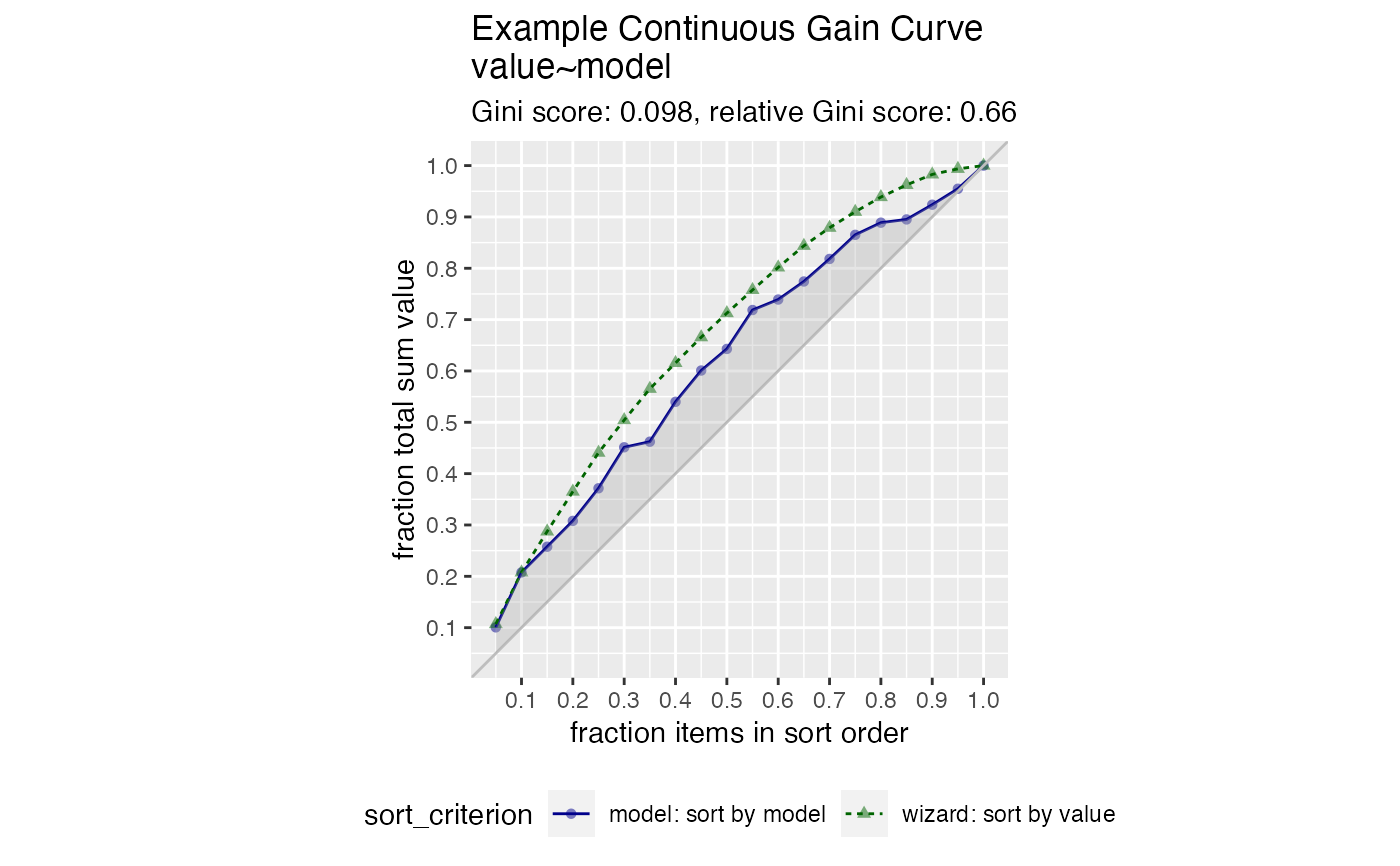
Plot the cumulative gain curve of a sort-order.

GainCurvePlot(
  frame,
  xvar,
  truthVar,
  title,
  ...,
  estimate_sig = FALSE,
  large_count = 1000,
  truth_target = NULL,
  model_color = "darkblue",
  wizard_color = "darkgreen",
  shadow_color = "darkgray"
)

Arguments

frame	data frame to get values from
xvar	name of the independent (input or model score) column in frame
truthVar	name of the dependent (output or result to be modeled) column in frame
title	title to place on plot
...	no unnamed argument, added to force named binding of later arguments.
estimate_sig	logical, if TRUE compute significance.
large_count	numeric, upper bound target for number of plotting points.
truth_target	if not NULL compare to this scalar value.
model_color	color for the model curve
wizard_color	color for the "wizard" (best possible) curve
shadow_color	color for the shaded area under the curve

Details

The use case for this visualization is to compare a predictive model score to an actual outcome (either binary (0/1) or continuous). In this case the gain curve plot measures how well the model score sorts the data compared to the true outcome value.

The x-axis represents the fraction of items seen when sorted by score, and the y-axis represents the cumulative summed true outcome represented by the items seen so far. See, for example, https://www.ibm.com/support/knowledgecenter/SSLVMB_24.0.0/spss/tutorials/mlp_bankloan_outputtype_02.html.

For comparison, GainCurvePlot also plots the "wizard curve": the gain curve when the data is sorted according to its true outcome.

To improve presentation quality, the plot is limited to approximately large_count points (default: 1000). For larger data sets, the data is appropriately randomly sampled down before plotting.

Examples

set.seed(34903490)
y = abs(rnorm(20)) + 0.1
x = abs(y + 0.5*rnorm(20))
frm = data.frame(model=x, value=y)
WVPlots::GainCurvePlot(frm, "model", "value",
   title="Example Continuous Gain Curve")